Pierre Crespin

Quelques propriétés assez remarquables de ce pavé-pentagone :

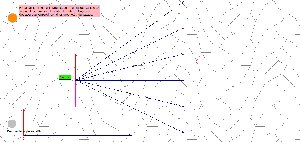
Tous ses angles sont des multiples de 15°. AnglesPenta15
Il est inscrit dans un triangle équilatéral. New penta tri
On peut obtenir un pentagone Penta15 assez simplement Penta15 new
0n peut aussi chercher un tel pentagone inscrit dans un triangle équilatéral donné : figure
Pour un pentagone ABCDE tel que présenté figure Penta 1502, dans une symétrie axiale par rapport au côté [AE], le pavé obtenu a un côté [C'D'] parallèle à [AB], et on a v(C'D') = v(AB) ainsi que v(CD) = v(AB') où v(AB) représente le vecteur AB.
D'où deux rectangles présents dans l'assemblage des deux pavés et deux translations potentielles pour conserver le pavage globalement invariant Penta 1502

On peut choisir une unité de longueur telle que tous les côtés aient une mesure rationnelle et un seul côté une mesure irrationnelle. Je prendrais 2 comme mesure du côté AE dans la figure initiale, trois autres côtés ayant alors pour mesure 1, et le dernier (BC) une mesure irrationnelle.

De même le nombre important, dans le pavage, de directions des côtés (10) et leur répartition régulière (multiples de 15° sauf pour deux manquantes) me semble contribuer à la richesse des décorations sur un unique pavage suivant la coloration des pavés. Du moins, c'est la première impression que j'en ai retirée sans trop de preuves à ce stade.

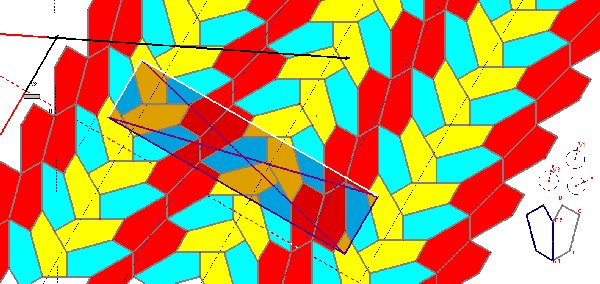
Voir des images du pavage du plan et les variantes possibles selon les choix des couleurs des pavés (pages 2, 2.1, 2.2)

Voir le diaporama "les diverses facettes du pavage" (Diaporama PowerPoint: Enregistrer le fichier et l'ouvrir pour le visionner)

Voir un tableau donnant les sommes des angles du pentagone

Voir une figure du pavage avec ses commentaires sur les éléments de symétrie (translations, symétries centrales et anti-déplacements).

Ces figures Cabri permettent d'entrevoir un peu les propriétés possibles lors de l'assemblage de deux ou plusieurs pavés.
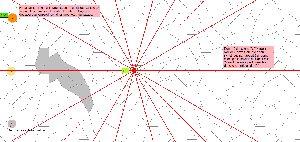
Ci-dessous des figures du pavage avec possibilité de voir quelques vecteurs et translations d'une part, et les directions des cotés d'autre part.